Denis McMahon:Have braking distances improved over time? I am not so sure. However good the driver or the brakes, ultimately it depends on the coefficient of friction between rubber and asphalt. Since this is a fairly innate physical feature, my guess is that it has not improved by much. I should be very interested if anyone has any reliable data on this. It is probably sensible to stick to the long-established figures for braking to stay on the safe side.
Oh gosh yes they've improved. First disc brakes and then ABS were quantum steps in braking improvement. But whether braking distances have improved significantly in, say, the last 30 years I'd agree is perhaps more open to question. They probably are improving incrementally due to improvements in tyres, road surfaces. Car weight would be a factor but I must admit I am confused as to whether this is typically higher or lower than it used to be! (see the article I reference below).
Putting our foot on the brake and the car coming gracefully to a halt in a controlled manner is something we take for granted so much now that it's easy to forget that many of us (who really aren't that old ?) used to have just put our foot down and hope - and it took considerable skill in slippery conditions. My worst ever experience - which was extremely frightening - was a braking distance of around 2 miles through the Peak District due to overheated drum brakes,,,,
Just found this article https://www.diaryofanadi.co.uk/?p=21456 which in turn refers to this one https://www.howardsgroup.co.uk/news/group/stopping-distance-is-the-highway-code-wrong which have a range of strong viewpoints and calculations on this issue. I was particularly amused that it says (I don't know whether is true or not) "A Ford Anglia [was] the car allegedly used to set the current numbers." Actually if so it would have been the version of the Ford Anglia prior to the one I learned to drive on, but certainly the one I learned on - drum brakes all round and no ABS - was an interesting object to try to slow down!
However, I very strongly suspect that the excellent braking of modern cars gives a false sense of security, and may well have caused drivers to drive faster without full awareness of the observing and thinking time factors.
Cheers,
Andy
Helios:
The speed idiots are probebely young kids thinking they are immortal ,last time I was on a motorway everyone was doing 90
Actually it's become clear that (in the UK at least) there are two groups, one is young people, the other is professionals in their 40s and 50s. From the last information I saw (this is rather from memory) this was across all driving practices that lead to the most common accidents - speeding, phone use, and drink driving.
After all, if you're a senior engineering manager you're a terribly important, clever and experienced person who knows much more about how to drive safely than some government bureaucrat. I'm sure we all know colleagues like that, although not ourselves of course ?
Cheers,
Andy
Simon Barker:
One advantage of the diagonal black bar is that the maximum speed limit may depend on what class of vehicle you may be driving. The speed limit for a truck can be different for a car on the same stretch of road. The black bar sign simply says "national speed limit applies from here on".
Thanks for your observation, Simon. The rule is drive at the lower of the indicated speed limit for the road and the speed limit for the vehicle in question. This has always been the case. Until fairly recently the max speed for a heavy goods vehicle on a single carriageway road was 40 mph. This was the case whether a national speed limit applied or another one, for instance 50 mph. There is no need for a special "national" sign to cater for this.
The so-called "national" sign dates back to when there was no speed limit on many open roads, and that is what it indicated then. It is understandable that when national limits were applied to all roads not subject to a lower limit, this sign was retained and redefined to its present meaning. This would have been fine as an interim arrangement, avoiding the need to replace a great many signs. I suggest the "national" sign is now well past its use-by date. This is just another example of the Government at snail's pace applying piecemeal amendment after amendment to our traffic regulations, culminating in the complicated arrangement we have now.
If we want to make things easier for all classes of vehicles and their drivers sharing the roads, perhaps we should consider the continental idea of indicating the speed limits for heavy vehicles on the back.
Benyamin Davodian:
Dear Rob,
I do not know how you calculated. Probably not understood. I suggest you again check you yourself because you mislead everyone
This is kinetic energy (180 kinetic energy requirements + 88 meters response time = 268 meters).
Distance difference from 100 km / h (real world test)
My dear Rob, you should check yourself where you went wrong.
Sorry, Benyamin but I agree with Rob. Per your earlier post, braking distance from 30 miles per hour is 45 feet not metres. 60 mph is 88 feet (not metres) per second.
As I said earlier, mixing of imperial and metric units leads to confusion.
Braking Distances
Kinetic Energy. Braking distance increases four times each time the starting speed doubles. This is because the work done in bringing a car to rest means removing all of its kinetic energy.
Work done = kinetic energy.
Work done = braking force x distance.
W = F x d.
Kinetic Energy = 1\\2 X mass X velocity2.
This means that:
F x d = 1/2 x m x v2
Therefore, for a fixed maximum braking force, the braking distance is proportional to the square of the velocity.
Question.
Calculate the total breaking distance of a car travelling at 12m/s, when the driver’s reaction time is 0.5s and they see a child run into the road?
Additional Information:
Car Mass: 900Kg.
Braking Force: 2000N.
Calculations:
Part 1. Reaction (Thinking) Distance:
Distance = speed x time.
d = v x t.
Therefore, d = 12m/s x 0.5s
Thinking Distance = 6m.
Part 2. Braking distance calculation:
F x d = 1/2 x m x v2
Transposed:
d = (m x v2)/f x (1/2)
d = (900 x 122)/2000 x (1/2)
Braking Distance = 32 metres.
Therefore, the total stopping distance is:
Stopping distance = Reaction distance + Braking distance.
Stopping distance = 6 + 32.
Answer: 38m
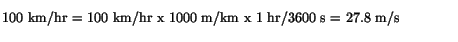
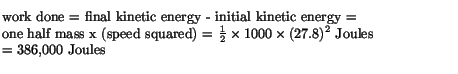
We're about to take you to the IET registration website. Don't worry though, you'll be sent straight back to the community after completing the registration.
Continue to the IET registration site