Thank you for the equation definitely covers a few misconceptions I was having ill look to put this into practice. 

So resistance and reactance can be seen as more indirectly proportional. And the fact that a smaller csa cable tends to have a lover current passing through it is the reason to which the reactance is lower due to the weaker Magnetic field been created would this be right? 

AJJewsbury said:

but supply and wiring system values? Or are they often insignificant compared with the load?

Typically, supply impedance is ignored for installations up to 100 A single-phase. For larger installations, reactance should be taken into account, and either:

 - Typical values will be provided by DNO or via other industry guidance (ENA Engineering Recommendations); or
 - The designer will determine from the transformers/generators used.

Typically cable reactance is ignored for cables up to and including 16 sq mm (or the very short lengths of 'tails' used in 100 A installations). Greater csa, it is advised to take cable reactance into account.
An exception is SWA cables, where even though the copper csa may be below 16 sq mm, the armour csa is typically above 16 sq mm, and has a more significant effect, and reactance should be taken into account for earth faults in SWA at least, even for copper csa up to 16 sq mm.

Please could you explain or highlight where you got this equation from 

Thank you 

the resultant of that of course is sqrt (.25^2 + .23^2)  or about 0.34 ohms, and at a touch off  45 degrees. (it would have been be 45 degrees if the two were exactly equal.)

Mike

which if I remember my O-level trig correctly means we can equally write it as:

0.3397 = cos(42.614º)*0.25 + sin(42.614º)*0.23

(perhaps slightly perverse in the immediate context, but might compare with the appendix 4 approach)

   - Andy.

yes, the appendix 4 seems to go out of its way to avoid mentioning complex phase, which is for me at least, a much easier way to visualise it.

M.

Would you please be able to highlight where you found this equation thank you. 

Please could you explain or highlight where you got this equation from 

this one?

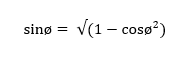
It's just a re-arrangement of the well known maths short-cut: sin²+cos² = 1

If you prefer, think of an right-angled triangle with a hypotenuse of 1. Pick one of the other angles, then sine of that angle give the length of the opposite side, cos of the same angle gives the length of the adjacent side. Then by Pythagoras - the square of the hypotenuse is equal to the sum of the square of the other two sides - so 1² = sin(angle)² + cos(angle)² - and 1² = 1 so sin(angle)² + cos(angle)² = 1.

   - Andy.

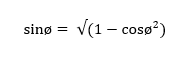(1)

Is Pythagoras - In a right angle triangle, the hypotenuse (side opposite the right angle) has a length that is the square root of the sum of squares of the other two sides. Neat proof here far better than I can draw it ;-)

Let us name the sides of that triangle a, b, h

Now as the sine of an angle is the length of  the side opposite it over the hypotenuse, (a/h) and the cosine is the side adjacent to it over the hypotenuse (b/h), then eliminating the hypotenuse by  cancellation we see that if

(a/h)^2+ (b/h)^2 =1 or (2)

(sin(x))^2 + Cos(x))^2=1 which is eqn 1 above.