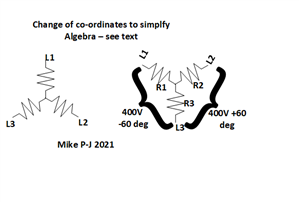
1. A load of 2.5kW takes a current of 12 Amp from a 230 Volt supply. Calculate the power factor.
2. Three single phase loads are to be connected to a three phase supply. All at unity power factor. The loads are,
i, 60 Amp.
ii, 50 Amp.
iii, 40 Amp.
By any method determine the neutral current.
Z.