
Paul Brewerton:
An d my instinct tells me that a measured Zs reading must be more accurate than a calculated one, since it will include all parallel paths under test.
Hello Paul,
The main problem to compare results of testing Zs and calculating Zs (and their respective SC-currents) is temperature of conductors. The temperature of conductors directly affects the test results (real temperatures at the moment of the test) or the calculation results (theoretically given temperature or temperature defined by standards).
SC-current calculation.
Calculation is needed to obtain the theoretical values of the largest and smallest SC-currents. According to IEC60909 the calculations of the maximum SC-current and the minimum SC-current shall be performed for each checked point.
For example the MeteorSPEC software gives the following results for 3-phase Cu 50mm2 cable L=100m and for transformer 400kVA D/Y:
Maximum 1-phase SC-current (temperature of conductors 90C) = 2.213 kA
Minimum 1-phase SC-current (temperature of conductors 20C) = 1.46 kA (a fragment of the calculation report is shown at the end).
SC-current test.
In common case you don’t know the temperature of conductors at the moment of the test. Usually the tested circuit consists from many cable sections that are installed differently and were loaded differently before performing the test.
You get some result, but you can’t say anything - can the SC-current be in this place at another time more or less than what you measured now.
Test versus calculation
Testing and calculation results cannot be directly compared. Calculation gives the theoretical possible boundary. Test results can confirm or not confirm the calculation results, nothing more.
Thus, for the correct selection of the protective device, it is necessary to calculate the SC currents at the end points (usually enough minimum current) of a feeder and obtain the results of tests (which should be greater than the calculated minimum currents).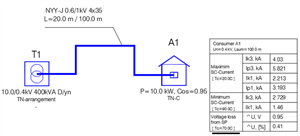
MeteorSpec-NETWORK DETAILED REPORT Minimum SC-current
Total length of cable = 100.0 m
Number of cables installed in parallel = 1
Phase Conductors = Cu 35.0 mm2
Resistance per unit length of phase conductor = 0.524 mOhm/m [20C]
Temperature factor of phase conductor metal = 0.00393 [1/.K]
Temperature of conductors = 90.0 C
Resistance per unit length of phase conductor = 0.6682 mOhm/m, [90C], IEC60909-0 [32]
Positive-sequence resistance of cable R ( 1 ) = 66.8215 mOhm, [90C]
Positive-sequence reactance per unit length = 0.0844 mOhm/m, [50Hz]
Positive-sequence reactance of cable X ( 1 ) = 8.4408 mOhm, [50Hz]
Return Conductor = Cu 35.0 mm2
Return by fourth conductor
Zero- and positive-sequence resistance ratio R ( 0 ) /R ( 1 ) = 4.0
Zero-sequence resistance of cable R ( 0 ) = 267.2861 mOhm, [90C]
Zero- and positive-sequence reactance ratio X ( 0 ) /X ( 1 ) = 3.8
Zero-sequence reactance of cable X ( 0 ) = 32.075 mOhm, [50Hz]
Z ( 1 ) = 66.8215 + j8.4408 = 67.3525 mOhm, [90C][50Hz]

Paul Brewerton:
An d my instinct tells me that a measured Zs reading must be more accurate than a calculated one, since it will include all parallel paths under test.
Hello Paul,
The main problem to compare results of testing Zs and calculating Zs (and their respective SC-currents) is temperature of conductors. The temperature of conductors directly affects the test results (real temperatures at the moment of the test) or the calculation results (theoretically given temperature or temperature defined by standards).
SC-current calculation.
Calculation is needed to obtain the theoretical values of the largest and smallest SC-currents. According to IEC60909 the calculations of the maximum SC-current and the minimum SC-current shall be performed for each checked point.
For example the MeteorSPEC software gives the following results for 3-phase Cu 50mm2 cable L=100m and for transformer 400kVA D/Y:
Maximum 1-phase SC-current (temperature of conductors 90C) = 2.213 kA
Minimum 1-phase SC-current (temperature of conductors 20C) = 1.46 kA (a fragment of the calculation report is shown at the end).
SC-current test.
In common case you don’t know the temperature of conductors at the moment of the test. Usually the tested circuit consists from many cable sections that are installed differently and were loaded differently before performing the test.
You get some result, but you can’t say anything - can the SC-current be in this place at another time more or less than what you measured now.
Test versus calculation
Testing and calculation results cannot be directly compared. Calculation gives the theoretical possible boundary. Test results can confirm or not confirm the calculation results, nothing more.
Thus, for the correct selection of the protective device, it is necessary to calculate the SC currents at the end points (usually enough minimum current) of a feeder and obtain the results of tests (which should be greater than the calculated minimum currents).
MeteorSpec-NETWORK DETAILED REPORT Minimum SC-current
Total length of cable = 100.0 m
Number of cables installed in parallel = 1
Phase Conductors = Cu 35.0 mm2
Resistance per unit length of phase conductor = 0.524 mOhm/m [20C]
Temperature factor of phase conductor metal = 0.00393 [1/.K]
Temperature of conductors = 90.0 C
Resistance per unit length of phase conductor = 0.6682 mOhm/m, [90C], IEC60909-0 [32]
Positive-sequence resistance of cable R ( 1 ) = 66.8215 mOhm, [90C]
Positive-sequence reactance per unit length = 0.0844 mOhm/m, [50Hz]
Positive-sequence reactance of cable X ( 1 ) = 8.4408 mOhm, [50Hz]
Return Conductor = Cu 35.0 mm2
Return by fourth conductor
Zero- and positive-sequence resistance ratio R ( 0 ) /R ( 1 ) = 4.0
Zero-sequence resistance of cable R ( 0 ) = 267.2861 mOhm, [90C]
Zero- and positive-sequence reactance ratio X ( 0 ) /X ( 1 ) = 3.8
Zero-sequence reactance of cable X ( 0 ) = 32.075 mOhm, [50Hz]
Z ( 1 ) = 66.8215 + j8.4408 = 67.3525 mOhm, [90C][50Hz]
We're about to take you to the IET registration website. Don't worry though, you'll be sent straight back to the community after completing the registration.
Continue to the IET registration site