Chris Pearson:Denis McMahon:.
Higher harmonics can also add, but they are less of an issue because they are much smaller.I gave this more thought as I was clipping my yew hedge this afternoon.
A flute produces something near a sine wave, but a clarinet does not. However, if the magnitude of any harmonic were greater than the fundamental, would that frequency not be the fundamental?
I then wondered what would happen if all the current were at the third harmonic. It seems fairly clear that now we simply have a supply at 150 Hz.
. . .
Isn't gardening therapeutic! Many of my inspirations come when I am in the shower.
Anyway, taking the points on sound waves. The sound of a clarinet is stronger in harmonics than that of a flute, so its waveform is less like a sound wave. The oboe gives even richer harmonics, thus more of a piercing sound. Now take a quite different instrument, the violin, where the harmonics are so strong and ordered that it is almost saw-tooth in shape.
If a harmonic had greater magnitude than a fundamental, would it not be the fundamental? My answer would be "no". The fundamental is by definition the lowest frequency. It usually has the largest amplitude but this does not need to be so. A telephone line cannot handle frequencies less than 300 Hz so low harmonics are suppressed. This makes a voice over the phone sound "thin". The fundamental of the human voice is less than 300 Hz; male speech fluctuates around 100 Hz. But the fundamental effectively "modulates" the higher harmonics. These modulations are heard over the telephone, and the brain can interpret them to derive the fundamental. So if, for example, someone sings over the phone, we can follow the fundamental pitch.
What if all the current were at the third harmonic? The harmonics are produced as a result of the response of the circuitry to the fundamental frequency of the supply p.d. The only way I could see all three phases at 150 Hz would be if that were the supply frequency. In which case, they would be fundamental frequencies, cancelling one another if equal, and the third harmonics would be 450 Hz.
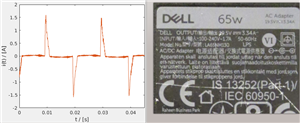
So now we have 100 A in two of the line conductors and 150 A in the neutral.
Denis McMahon:.
Higher harmonics can also add, but they are less of an issue because they are much smaller.
I gave this more thought as I was clipping my yew hedge this afternoon.
A flute produces something near a sine wave, but a clarinet does not. However, if the magnitude of any harmonic were greater than the fundamental, would that frequency not be the fundamental?
I then wondered what would happen if all the current were at the third harmonic. It seems fairly clear that now we simply have a supply at 150 Hz.
So now I wonder whether the triplen harmonic(s) can ever be more than 50% of the current.
Let's have a balanced load of 100 A per phase and 50% 3rd harmonic. 3 x 50 A at 50 Hz cancel out; and 3 x 50 A add up so we have 150 A in the neutral.
Now let's take a supply with 100 A on 2 phases and none on the third. The third harmonic accounts for 50 % of the current. So at 50 Hz, 50 A goes down the neutral.* At 150 Hz 2 x 50 A goes down the neutral. So now we have 100 A in two of the line conductors and 150 A in the neutral.
Doubtless the likes of Mike or OMS will comment if I am talking drivel. ?
* see Annex A722.
Chris Pearson:
. . .
Now introduce a harmonic at 150 Hz i.e. 3 times the fundamental. Because they are now going three times as fast, the vectors are not 120 degrees out of phase with each other, but in phase so they add up.
. . .
Very succinctly put, Chris! I was trying to think of a way to put this over simply but you've beaten me to it.
Over the past several years I have seen in IET journals references to rectifiers, switch-mode supplies, thyristors, etc. and the effect that the wave chopping of these ever-increasing devices will have on the power supply. Effectively, these chopped current waveforms are a series of harmonics. The third harmonic is particularly troublesome because of the way in which the waveforms add up and augment one another on the neutral. Higher harmonics can also add, but they are less of an issue because they are much smaller.
I think these harmonics are becoming a part of life, though in this instance they are larger than I would expect. In the case of this installation, a proper analysis would require to display the current waveforms of each of the phases on an oscilloscope and assess the extent of the harmonic distortion.
We're about to take you to the IET registration website. Don't worry though, you'll be sent straight back to the community after completing the registration.
Continue to the IET registration site