
Hi I am working through equation 6 for an ambient temperature of 50 degrees for 1mm 90degC thermoplastic cable (Table 4E2A)
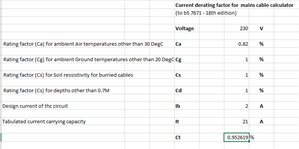
I get a correction factor of 0.95 for a 2A load.
Do i divide the mV/A/m by this factor ?
The text says multiply, but that would mean the resistance decreases with the increase in temperature (or have I got the sum wrong?)

