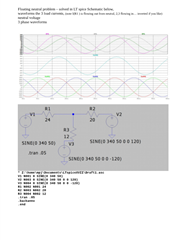
I am afraid my electrical engineering princIples are letting me down.
So if I have a standard 400/230v star connected secondary feeding an installation that comprises 3 single phase loads of 10A, 12A and 20A for L1, L2 and L3 respectively, all in phase, no harmonics. I estimate the neutral current to be 9.16A. If I lose the neutral upstream of the loads what is the voltage to earth? Is it less than 55v?