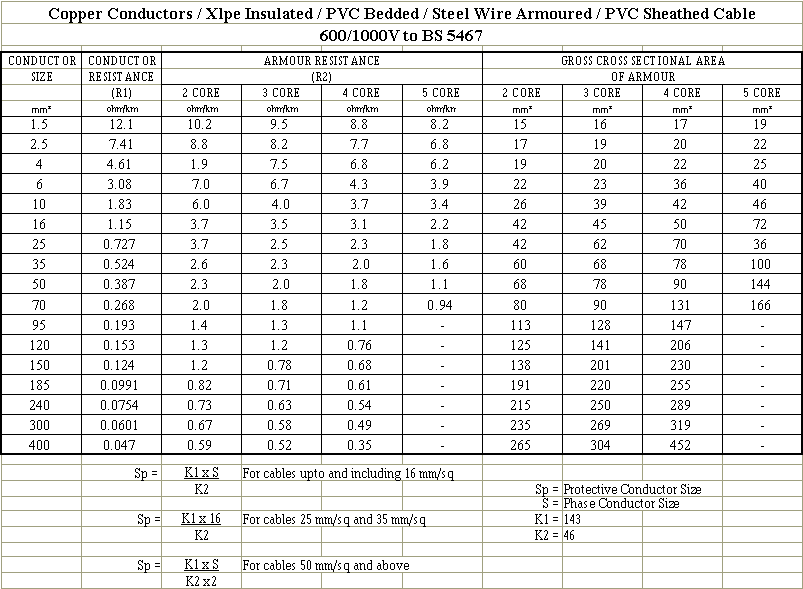
While on a site last week, I noted 25mm2 4-core swa cables being installed on a ladder and for some reason, each one had a 10mm2 separate copper cpc cable tied to the swa. The furthest run is about 50m from a DB where the EFLI is 0.1 ohms.
Just as an academic exercise, I set about trying to establish the current division between the wire armour and the separate 10mm2 copper cpc using the formulae in the IET Design Guide. Factoring in the usual temperature increases, 70 for phase in the swa, 60 for the wire armour and 30 for the separate cpc, the expected impedance was 0.25 ohms with a fault current (using 230) of 1140A dividing to 672A in the wire armour and 826A in the separate cpc.
Data used; R1 at 20C = 0.73mohms, R2a at 20C = 2.1mohms and R2p at 20C = 1.83mohms. Likely there is no real merit in the pedantic adjustment for temperature, but hey!
If someone felt sufficiently bored and had an old fag packet, would they be kind enough to check my results? Strangely, if one reduces the separate cpc to 2.5mm2 the fault current is 936A dividing to 244A in the wire armour and 727A in the 2.5mm2 separate cpc. That is counter intuitive but perhaps expresses a limitation on the formulae or, much more likely, a limitation on my understanding!