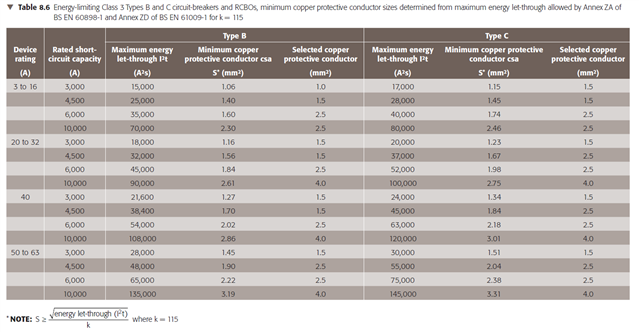
When using the Adiabatic equation, only to calculate the minimum size CPC, I am thinking that using the fault currents given in Appendix 3 of BS7671 rather than that calculated (UO/ZS) would give a more realistic outcome.
For example: A D6 circuit breaker is protecting a circuit where the calculated fault current is 328A. The table associated with Fig 3A6 in Appendix 3 of BS7671 shows that an overcurrent of 120A will operate the 6A breaker in 0.4s. Using these values and a K value of 115 results in a minimum CPC of 0.66mm2 (1.0mm2), whereas if you use the 328A the calculation results in a minimum CPC of 1.80mm2 (2.5mm2).
I cannot see a problem with using the lower value, but would appreciate confirmation and guidance from others.