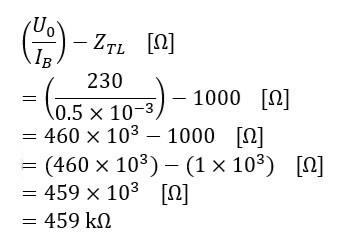In Guidence Note 8 where the equation 6.1 is used to illustrate the range of values of resistance RCP for the currents IB of 0.5mA, 10mA & 30mA in equations 6.2, 6.3 & 6.4, what is the second value of 1000 thats deducted from the value of RCP for? Looking at equation 6.1 the first value of 1000 thats deducted is for the impedance of the human body ZT taken to be 1000Ω from BS IEC 60479-1:2018 for the purpose of this calculation, but I'm struggling for this moment to understand what the subtraction of the second value of 1000 is for?
It looks to me like the equations have been incorrectly printed and the sum of each should be 459,000Ω, 22,000Ω & 6670Ω respectively and the second value of 1000 should be dividing the sums by 1000 to convert the values to KΩ?
If this is the case then these equations have been miss printed and miss represented in GN8 for the last 20+ years! Not to mention the publications and documents that they've been copied across to over these years...
Any thoughts on this would be much appreciated...