Hello All,
Just reading this nice article on PEN protection:
https://electrical.theiet.org/wiring-matters/years/2021/84-march-2021/broken-pen/
Looking at implementing PEN protection as per BS7671: 722.411.4.1 - section (iii), which I believe allows for deriving a virtual neutral, which I thought could be done by looking at the L -> N phase voltages.
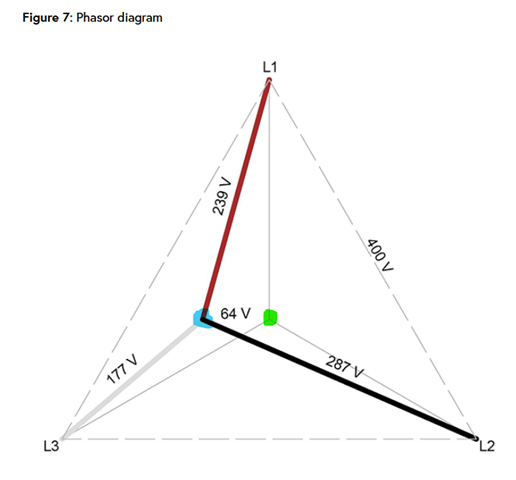
Figure 7 in that article shows a phasor diagram where L1, L2, L3 are 239V, 287V, 177V respectively, and shows a neutral shift of 64V. However if those phases are vector added assuming 120 degree phase shift, it's more like 95.5V. I had to tweak the phase shift somewhat to get close to the 64V (0, 232, 113 degrees for instance).
Just wondering if my thinking is wrong, or in the event of a PEN fault could phase shift occur?
Thanks in advance.
Marty.