So I have been down a rabbit hole for some time now and need a bit of clarification.
Possibly someone might be able to explain Fig 15B - Radial final circuit arrangement
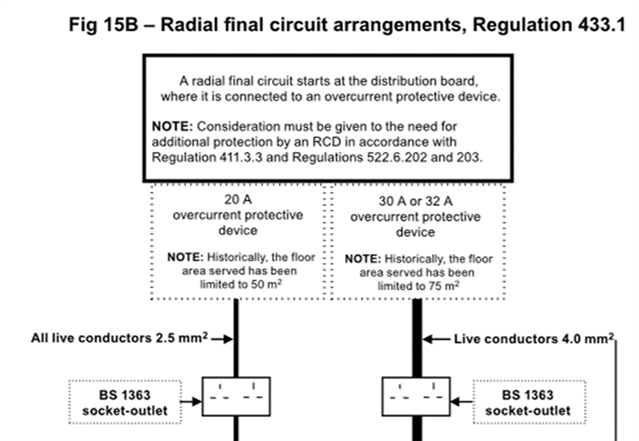
it's suggested that 4.0/1.5mm cable could serve a 75 m2 on a 30A or 32A CB
what would the length be of that cable?
when I perform a voltage drop calculation the length of the cable is 32m which is no where near 75m.
The OSG mentions that the max length for a radial on a 32A CB is 43m with an assumed load of 26A.

Anyone able explain how 75 m2 in fig 15B has been worked out, surely there should be a not stating what length cable its equivalent to.
on a separate note what if the radial circuit was supplying 1 x 13A socket, is there an equation to work out the overload allowance of a circuit or is it simply Ib < In < Iz?
if so then what would the maximum load be expected on a 13A socket? there's nothing stopping someone plugging in an extension lead or adaptor to increase the load.