Hello
I have a basic question on touch voltage. I just can't seem to grasp it..
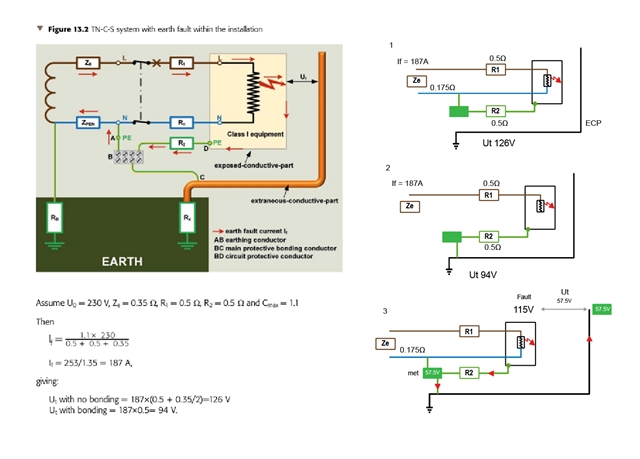
This is taken from guidance note 5
I have attached 3 sketches alongside .
1 and 2 are as GN5 describes
The third is my confusion.
1 & 2. We calculated touch voltage, in this case 126V without MPB and 94V with MPB
Now I understand I think the basic concept the greater the resistance , the higher the voltage current being constant
Number 3, is How I imagine it...
We have a fault and at the Exposed CP we have a voltage of say 115V
The resistance of the CPC to the MET will reduce this voltage again to say half again so 57.5V at the MET
Since we have MPB connected to the MET . The MET and Extraneous part will be roughly at 57.5V
So our touch voltage would be between the EXP and EXT conductive part so.115V ---- 57.5V A difference of 57.5V
I don't understand in the GN5 examples, Why is touch voltage is one amount?
126 volts to what? To Earth?
But since the MET will be at a raised potential It can't be to earth?
Hope that makes sense.