Rules and Guidelines
Want to participate in the discussions? Please read our Community Rules and Guidelines. Need some help? Visit Support and Answers.

  • State Not Answered
  • Replies 15 replies
  • Subscribers 40 subscribers
  • Views 566 views
  • Users 0 members are here
Options
You may also be interested in

Adiabatic Equation

Horace Charles

I am not an electrician but have a personal technical interest in understanding the Wiring Regulations.

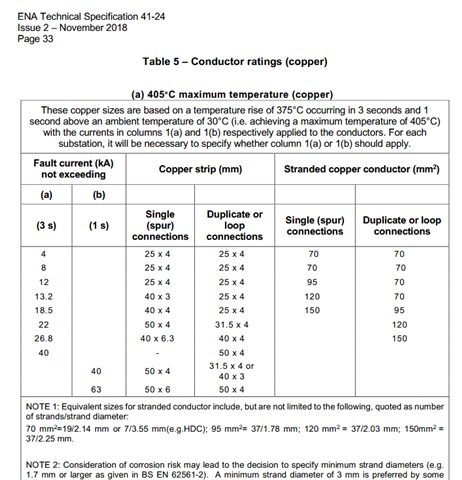
I have become a bit confused by some contributions on the internet which seem to suggest that the adiabatic calculation will determine the size of CPC that will "cope with" a temperature rise to the maximum temperature permitted for a given cable type.

But as I understand it, it is the insulation which has to tolerate the temperature rise. This rise is caused by the heating effect (IsquaredR) of the current flowing in the CPC (and live conductor) under a dead short earth fault condition and which flows for the time it takes for the overcurrent protective device to disconnect the supply. Exceeding the maximum permitted temperature would permanently damage the insulation which I assume would no longer insulate.

Outside the parameters of the adiabatic conditions I assume that the conductors themselves could tolerate a very much higher and longer duration current, and hence temperature rise, before they themselves would become damaged. The only damage I can think of is that an unprotected conductor would melt like a fuse.

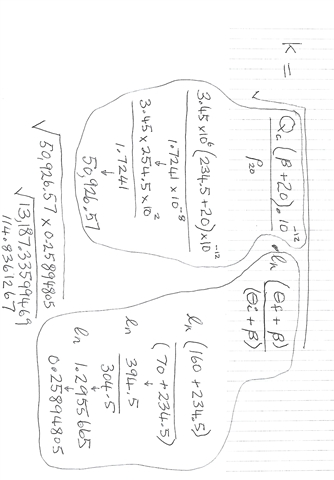
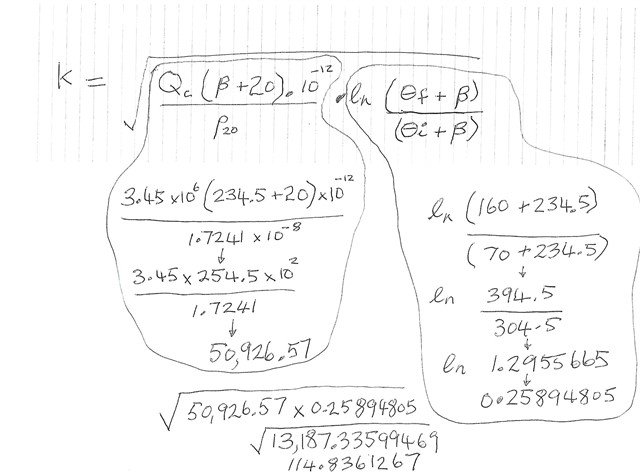
But for the adiabatic conditions of a known maximum level of earth fault current and a known OCPD disconnection time, the equation will determine the minimum size of CPC which would generate a temperature rise in the cable to the maximum permissible temperature for the insulation. In the case of a multi core cable like twin and earth, I assume that for an earth fault the heat contribution from the live conductor is not considered because the contribution from the smaller and hence higher resistance CPC will be much greater and more significant.

I will be pleased to hear from expert readers to confirm or otherwise clarify if I have understood the theory of this correctly . Thanks

Parents
  • 0

    But as I understand it, it is the insulation which has to tolerate the temperature rise. 

    Correct (the consideration is not just for the metallic conductor alone but also what's around it that sets the limit on acceptable temperature rise) - and that requirement is captured in the differing values for "k" (as per tables 54.2 to 54.6)

    The only damage I can think of is that an unprotected conductor would melt like a fuse.

    Or thermally damage the supports (think bare bus-bars) or even damage to the conductor's surroundings - e.g. setting fire to adjacent materials.

       - Andy.

  • 0 in reply to AJJewsbury

    Thank you @gkenyon, @Simon Barker, @mapj1 and @AJJewsbury for your feedback. 

    I'm digesting your comments and studying a bit more before I ask any further questions about them.

    In the meantime thanks

  • 0 in reply to Horace Charles

    Mean while, although no figures  for hot bare copper, are in the wiring regs BS7671 it is interesting to look at the figures the ENA use for DNO type wiring at substations.
    Bare strips and bare stranded wire can be  used for earth bond interconnections to electrodes and between enclosures & so on.

      This table suggests that the  (smallest )bare copper 70mm2 cable is good for at least 8000  amp faults  for 3 seconds, but there is no insulation to damage. Note that at the end of the 3 seconds, the copper is at 405C - a temperature that would be put any kind of plastic insulation beyond use. The same document recommends no more than   325C for aluminium cored wire, and 400C for galvanized steel parts and a 250C rise for exposed bolted contacts however,...

    These are far higher fault current ratings than 'normal' can only be safely used when there is no part in contact that would be damaged by the heat. In a controlled location like a substation this is practical , as only competent persons are installing things, and the dangerous bits are in a locked compound or box, but even so if it were much hotter it would  leave scope to set fire to leaves, dust  or cobwebs, and as it is there are considerations of thermal expansion and stress on joints - hence the reduced limit on bolted connections  !.

    ref https://www.ena-eng.org/ENA-Docs/D0C3D1R/TS_41-24_181106101835.pdf
    regards Mike

  • 0 in reply to AJJewsbury
    I'm still studying about the adiabatic equation and in so doing I've learned a bit more about the way the K factors which appear in the regs have been calculated. This is a level of detail a bit removed from my original query but is all adding to my understanding.
    I found an old entry of yours (screenshot) giving the formula used. I wrote this out on two sheets of paper (attached) and sure enough it works. I used the case of thermoplastic pvc rising from 70 to 160 degrees, k=115
    I'm still studying just to satisfy my technical curiosity but for the moment the derivation of the formula and some of the parameters used (e.g. the reciprocal of the temperature coefficient) is beyond my existing knowledge of the physics.
    I'll return to my original query when I've got my thoughts together 
    Thanks to all respondents 
  • 0 in reply to Horace Charles

    Sorry forgot to rotate the scan

  • 0 in reply to Horace Charles

    How nice to see some proper scribbling! :-)

  • 0 in reply to Chris Pearson

    Indeed.

    It may help to consider the example of  a particular cable size, say 2.5mm2 and do a 'no text book' estimate.

    First the no of grams of copper in a 1m length of that cable  which is 2500 cubic mm, or 2.5 cc at  about 9 grams per cc so 22.5 grams) and the electrical resistance of that 1m length (about 7,5 milliohms).

    And there you have all the bits you need.  

    The energy to raise 1 gram of copper through  1 degree is about 0.38 joules, so to raise 1 gram of  it by 90C is 34Joules or 34 watt seconds. but of course we have 22,5 grams, so 760 watt seconds for that 70C to 160C rise. 

    Note that watts /R has the units of I2t.

    760 /0.0075 ~ 100,000. 

    Note he book value is normally taken as 77,000 so we are about 20%  out, but there has been some pretty casual rounding and we have nor allowed for the resistance rising when hot. 

    However, this is the same approach, just with all the steps showing.

    Mike.

  • 0 in reply to Horace Charles

    For copper, the square root of the first bit to the left of ln is always 226. So, its only the square root to the right of ln that needs to be determined before multiplying. 

    In your calculation, square root of the right hand side (0.258948) is approx 0.51 and 0.51*226 = approx 115.

    At least that is how, I do it. 

    By the way, the left for aluminium is 228 and steel 202.

  • 0 in reply to mapj1

    Thank you Mike for your reply with the example of a 1 metre length of 2.5mm2 copper cable.

    I'm working from first principles and here's what I understand from the figures you have used.

    The density of copper is approx 9 grams per cubic centimetre so for the 1 metre length of cable whose volume is 2.5 cubic centimetres, its approx. mass is 9 x 2.5 = 22.5 grams.

    The specific heat of copper is approx 0.38 joules per gram per degree C so to raise the temperature of the 1 metre length by 90 degrees will require 0.38 x 22.5 x 90 =approx. 760 joules which is 760 watt seconds.

    The next entry re watts/R having the units I2t has got me a bit confused. Did you mean watt seconds/R, that is, joules/R ?

    I had understood that Power = I2R = joules/second which if rearranged becomes joules/R = I2t

    So 760 joules is generated in the 0.0075 ohm of resistance by an I2t value of 760/0.0075 =approx. 100,000

    I'm sorry but I don't understand the note about the book value being 77,000, where does this figure come from?

    I understand the point about rounding errors and resistance increases due to temperature.

    As an experiment I inserted these values into the rearranged adiabatic formula to see what value of k they would produce.

    K = sq. root I2t/2.5 = sq.root 100,000/2.5 = 126.5

    Quite a way off from 115.

    Thanks again and I hope I have correctly understood the information you have provided

Reply
  • 0 in reply to mapj1

    Thank you Mike for your reply with the example of a 1 metre length of 2.5mm2 copper cable.

    I'm working from first principles and here's what I understand from the figures you have used.

    The density of copper is approx 9 grams per cubic centimetre so for the 1 metre length of cable whose volume is 2.5 cubic centimetres, its approx. mass is 9 x 2.5 = 22.5 grams.

    The specific heat of copper is approx 0.38 joules per gram per degree C so to raise the temperature of the 1 metre length by 90 degrees will require 0.38 x 22.5 x 90 =approx. 760 joules which is 760 watt seconds.

    The next entry re watts/R having the units I2t has got me a bit confused. Did you mean watt seconds/R, that is, joules/R ?

    I had understood that Power = I2R = joules/second which if rearranged becomes joules/R = I2t

    So 760 joules is generated in the 0.0075 ohm of resistance by an I2t value of 760/0.0075 =approx. 100,000

    I'm sorry but I don't understand the note about the book value being 77,000, where does this figure come from?

    I understand the point about rounding errors and resistance increases due to temperature.

    As an experiment I inserted these values into the rearranged adiabatic formula to see what value of k they would produce.

    K = sq. root I2t/2.5 = sq.root 100,000/2.5 = 126.5

    Quite a way off from 115.

    Thanks again and I hope I have correctly understood the information you have provided

Children
  • 0 in reply to Horace Charles

    The 'book value' is in a number of publications that seem to self reference , guide to the regs, wiring matters article etc.

    I'm not sure why its that much lower, but the point is that apart from the mangling of units (joules per ohm into A2t)  and having square roots that mean the constant does not immediately have units that relate to an obvious physical quantity, what we are looking at is the same.- I was trying to show the physics under the wrappers as it were.

    Mike. 

  • 0 in reply to mapj1

    Thanks Mike for your expert feedback which is much appreciated and has added to my understanding. I will keep studying this topic. Thanks

Community Rules & Guidelines