Rules and Guidelines
Want to participate in the discussions? Please read our Community Rules and Guidelines. Need some help? Visit Support and Answers.

  • State Helpful Answer
  • Replies 6 replies
  • Subscribers 38 subscribers
  • Views 115 views
  • Users 0 members are here
Options
You may also be interested in

Adding up current

JohnE

In a ring final circuit
(Based on Paul Cooks commentary of the 17th edition)

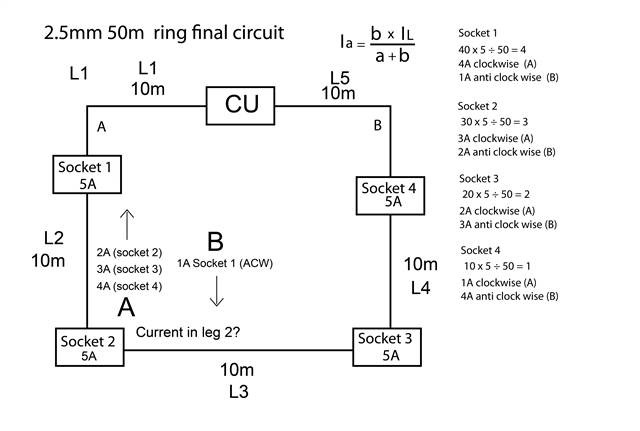
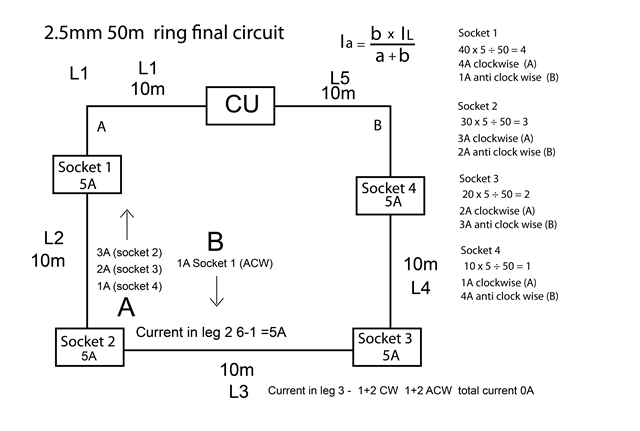
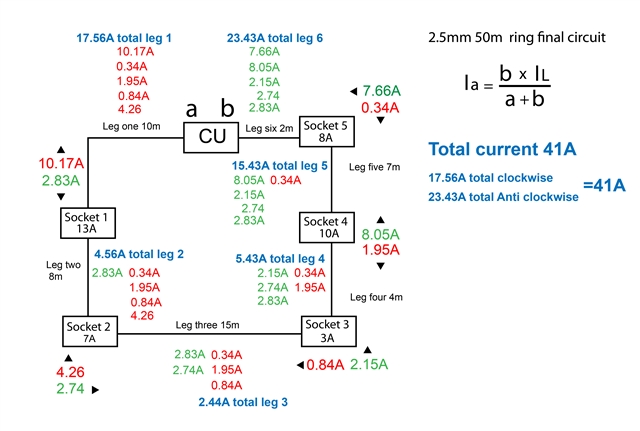
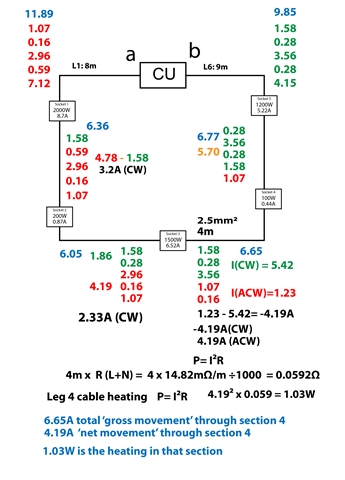
Very simple curent split using both legs of the ring

Not sure about adding up the currents in each leg
Take leg 2 Than will have the Ia of sockets 4,3 and 2
and the Ib of socket 1
How do these add up so you know the current in this leg?
Hope that makes sense
Thanks


  • +1

    You need to take the direction of the current (clockwise or anticlockwise) into account. E.g. 5A clockwise plus 3A anticlockwise on a given bit of cable gives a nett value of 2A clockwise. (Mathematicians would pick one direction as positive and so currents in the opporite direction are treated as -ve, so adding up works out).

    Taking a step back, the whole example is symmetric - same loading and same cable lengths - the left is an exact  mirror image of the right, so the currents must also be symmetric - anticlockwise current in L1 must be the same as the clockwise current in L5, likewise anticlockwise L2 must be the same clockwise L4 and so likewise clockwise L3 must be the same as anticlockwise L3 - i.e. L3 must be carrying zero current. If L3 carried any current it wouldn't be symmetric any more. Not true for the general case where loadings aren't so regular, but give you a way of sanity checking your calculations in this particular case.

       - Andy.

  • 0

    Thank you very much

    OK thats what I was curious about if the currents cancel out.
    So leg three would have 3A clockwise and 3A anti clock wise, so no current as you say.

    I see my initial sketch was incorrect
     Leg 2 would have 5 amps

    CW 1A, 2A, 3A  and ACW 1A  so a total of 5A

    I will put together a more realistic sketch

  • +1 in reply to JohnE

    John, I think that it may help if you have different loads at each socket. Try 4, 6, 8, and 10 A. The resistance of the cables is much lower than the loads, so that may be ignored.*

    It may also help to turn on one socket at a time. So 4 A at socket 1 would be 2 A acw in leg 1 and 2 A cw in legs 2 to 5. Etc.

    *ETA: my apologies - that is incorrect.

  • 0

    Thanks will have a go at what you suggest as well

    Ive done this one, total currents seem to add up !

  • 0 in reply to JohnE

    John, that looks good except that you have overloaded your ring with 41 A. :-) Leg 6 may run a bit warm unless it is clipped direct (Table 4D5).

  • 0 in reply to Chris Pearson

    The current share from each socket left or right is in proportion to the two resistance from that socket (lets call them clockwise and anti-clockwise paths) to the point of junction at the CU.

    There are two (low) resistances in parallel, between two places where the  voltages in the 2 wires are forced equal - both wires have to be at the same voltage at the socket because they meet at the terminals, and similarly the other ends of both wires are at the same voltage as each other (but slightly higher voltage than at the socket) once more at the CU,   

    So a socket half way round (in resistance terms, only half way in length if there are no changes of cable size.) sends half its load current either way.

    A socket at 9 O clock on the ring, sends 3/4 of its current on the short path, and 1/4 on the long. etc,.

    You can solve for the clock and anticlock -wise currents at each socket on its own first, then overlay and sum the answers for each segment.

    Mike.

Community Rules & Guidelines